Understanding Anthropic’s “Scaling Monosemanticity: Extracting Interpretable Features from Claude 3 Sonnet” and its implications for controlling models
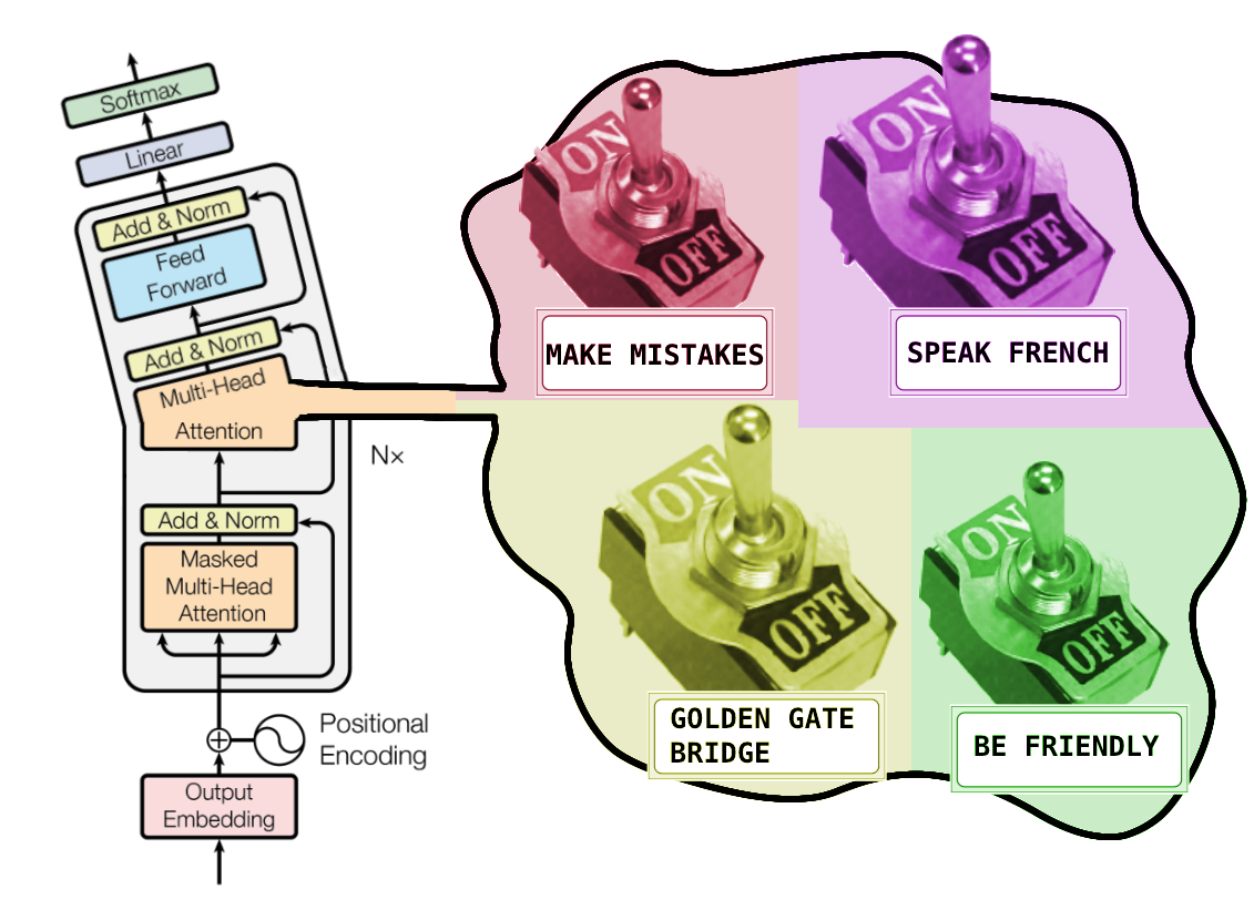
TL;DR Anthropic has shown there are clusters of neurons in LLMs that activate for specific behaviors and contexts. Features like “Coding Errors”, “Golden Gate Bridge”, or “Languages in Cyrillic script”. These are both read and write. When the model produces a coding error the “Coding Errors” cluster lights up. When you force this cluster off… it stops coding errors. This is a path towards controlling and interpreting LLMs - a future exists where models include switches to activate/inhibit different behavior.
Original monosemanticity paper and scaling monosemanticity paper.
In October of 2023 Anthropic released “Towards Monosemanticity: Decomposing Language Models With Dictionary Learning” showing you could create interpretable features to understand and control LLM. Recently, they followed up by scaling these discoveries to an actual production model. Let’s start with the original work.
What Anthropic Did To Interpret LLMs
This is a rough outline of their original monosemanticity paper methods. For now let’s think of the quest for monosemanticity as finding networks where one neuron controls one concept.
- They trained a single layer decoder only transformer (attention block + feedforward block) on The Pile (100 billion tokens). The hidden state of the model 512 features (dimensions). As a point of comparison Gemma 2B has a hidden state of 2048, 17 more layers, and is trained on 2 trillion tokens.
- They trained a Sparse Autoencoder (SAE) to encode model activations. Sparsity will be an important part of this system. Main focus is on a SAE 8x larger than the transformers dimensionality ($512*8=4096$).
- In a manually/AI assisted way, they anotate each of the SAE’s neurons.
Steering model behavior
Once you train a monosemantic model, you can steer the original models behavior.
- During training they measure the range of activations of each feature to get a maximum.
- To steer a feature, they multiply it’s corresponding neuron’s maximal activation by a constant in range [-10, 10]. Instead of feeding the transformer’s activations forward our controlled SAE is fed the hidden state. State get’s autoencoded but now a feature changed (so the autoencoding output should lack this concept’s attributes). Next layer gets the modified hidden state and the rest of the model finishes up.
So, what’s actually happening here?
Let’s breakdown what anthropic has done.
Monosemanticity, or one neuron per concept
The point of all of this is to figure out ways to have monosemantic (“mono” is one and “semantic” is meaning so one meaning) neurons. This just means that each neuron would control exactly one concept: there would be a neuron for each language, a neuron for comedy, a neuron for accuracy, neurons for landmarks (a golden gate bridge neuron), etc…
It turns out you can train a network on top of an LLM to do just that.
Sparse Autoencoders create more interpretable representations
An Autoencoder (AE) is a model that attempts to reconstruct its input. This is done by using a training loss that includes reconstruction error. Specifically, they use L2 loss:
$$L2=\Vert x-\hat{x}\Vert_2^2=\sum_i^n(x_i-\hat{x_i})^2$$
such that $x,\hat{x}\in\R^n$ where n is our transformers activation dimensions (512) and $\hat{x}=AE(x)$. Note that 0 loss would imply $\hat{x}=x$ $\forall x\in\R^{n}$. In other words, if we train a perfect AE, given any input (in our case transformer hidden activation), we will output our input.
This might not seem too useful at first (why would you want to output the same thing?). The trick is that our AE is a three layer MLP (input, hidden, and output) where our hidden layer will have a much larger dimensionality than its input and output. These last two must of course be the same dimension to be able to perform reconstruction. By having our hidden layer be a much larger size, we’re projecting our small N-dimensional input to a large M-dimensional (where M is some multiple of N) space. This larger representation space can be much easier to interpret since it lets us “separate out” the overlapping features that appear in inputs using sparcity. In other words, we’re inducing or trying to induce monosemanticity.
We won’t dive into the theory of why we want sparsity in our AE, but the idea is that by forcing the least number of neurons to fire in our M-dimensional space, we’re hoping that different features will activate different, separate neurons. If we weren’t using sparsity an activation would likely activate many more neurons.
To create sparcity, we add an L1 loss term which weighs on the absolute value of weight size (created by using ReLU activation). Let’s walk through each formulation, as taken from the follow-up scaling paper. Let’s start by considering our reconstruction:
$$SAE(y)=D(U(y))=D(\sum_i^nf_i(x))$$
Where $U$ is the “Up” projection $\R^n\rightarrow\R^m$ and D is the “Down” projection $\R^m\rightarrow\R^n$. Scaling monosemanticity calls each “Up” output a feature $f_i$. In ML terms, the “Up” projection is just a standard linear layer with ReLU activation which also promotes sparsity, and the “Down” projection is a linear layer.
$$L1=\lambda\sum_i^nf_i(x)\Vert W^D_{,i}\Vert_2=\lambda\sum_i^nf_i(x)\sum^m_j(W^{D}_j)^2$$
Where $\lambda$ is some small constant, and $W^D\in\R^{m\times n}$ are the “Down” projection weights.
Note that all we’re doing here is summing the product of our “Up” projection (normal L1) $f_i(x)$ and the L2 norm of our “Down” projection weights. The paper interprets the normalized weight of each feature as a direction for the feature. The main reason we include our “Down” projection weight in our L1 loss is that if we didn’t the model could in theory just make our features very small but spread out the weights as it chooses, defeating the purpose of looking for sparcity. The product $f_i(x)\Vert W^D_{,i}\Vert_2$ is what we’ll call our “feature activation”. We’ll consider this product to be how activated a feature gets given some transformer hidden activation.
Features, simplified
Our SAE is projecting one of our transformer layers hidden activation to a larger, sparse space. Each dimension/neuron has a measurable feature activation given inputs. Since our SAE is sparse, the default is that no neurons will fire given input. Any activations are interesting and worth exploring.
To interpret features, Anthropic fed text into the main transformer. For each neuron activation, they collect the tokens/token areas that activate them the most. From this, they can begin guessing/interpreting what each feature might mean.
Controlling models with features
For any input, we know that $$x=SAE(x)+L(x)=SAE(x)+(SAE(x)-x)$$
L is just our models loss (the difference between our desired output and our output). We could feed $SAE(x)+L(x)$ into the next transformer layer and it would change nothing in our LLM. The trick is that we can clamp the value of the feature we want to change to some set value that’s a multiple between [-10, 10] of the observed maximum during training. Negative values stop the feature manifesting and positive values promote it.
After clamping our SAE neuron, we feed $SAE(x)+L(x)$ into our next transformer layer, but note that $SAE(X)$ will now be changed in precisely the way that we’ve decided, steering the models output. It turns out that this method is fairly effective.
The scaling paper did this for a large LLM, where they add the SAE in a middle layer of the LLM.
Does it work?
Golden Gate Claude is one of the most personality infused LLMs we’ve seen.
Last chance to try Golden Gate Claude! Don’t miss out. https://t.co/1NiPPv2wea pic.twitter.com/ZwfNt9IQDm
— Kristi Hines (@kristileilani) May 24, 2024
We’ll likely have sliders that will specifically control model behavior
This should hopefully remove some of the blackboxiness of LLM’s. A couple of the interesting consequences of this research are:
- LLM’s likely work by creating linear combinations of concepts.
- We can find where these concepts exists.
- Just because a single concept is represented in multiple places does not mean we can’t create an intermediate one neuron representation (monosemanticity).
Overall, this is a very exciting time for model interpretability.